使用比特币私钥对任意消息签名

发表于 | 分类于 | 阅读次数：

在双钥系统中，签名可以作为身份认证和授权的手段。

  • 对签名方，能提供正确的签名，就意味着他一定有私钥
  • 对验证方，验签通过即可保证，消息内容未经篡改，且消息来源可靠

在比特币中也一样，我可以向你提供下列信息，来证明该地址属于我。

项 内容
地址 1AfxgwYJrBgriZDLryfyKuSdBsi59jeBX9
消息 你好世界
签名 H9DnqMSGQmqi0zIWQqVfPXQsq59Qt11F1rUQDxv+4/iUDrSLJ6xHZ7PUSKvVThVWQAy/lLEpE3JeMpOlwUiVGlo=

使用钱包工具或第三方服务，任何人都能验证。

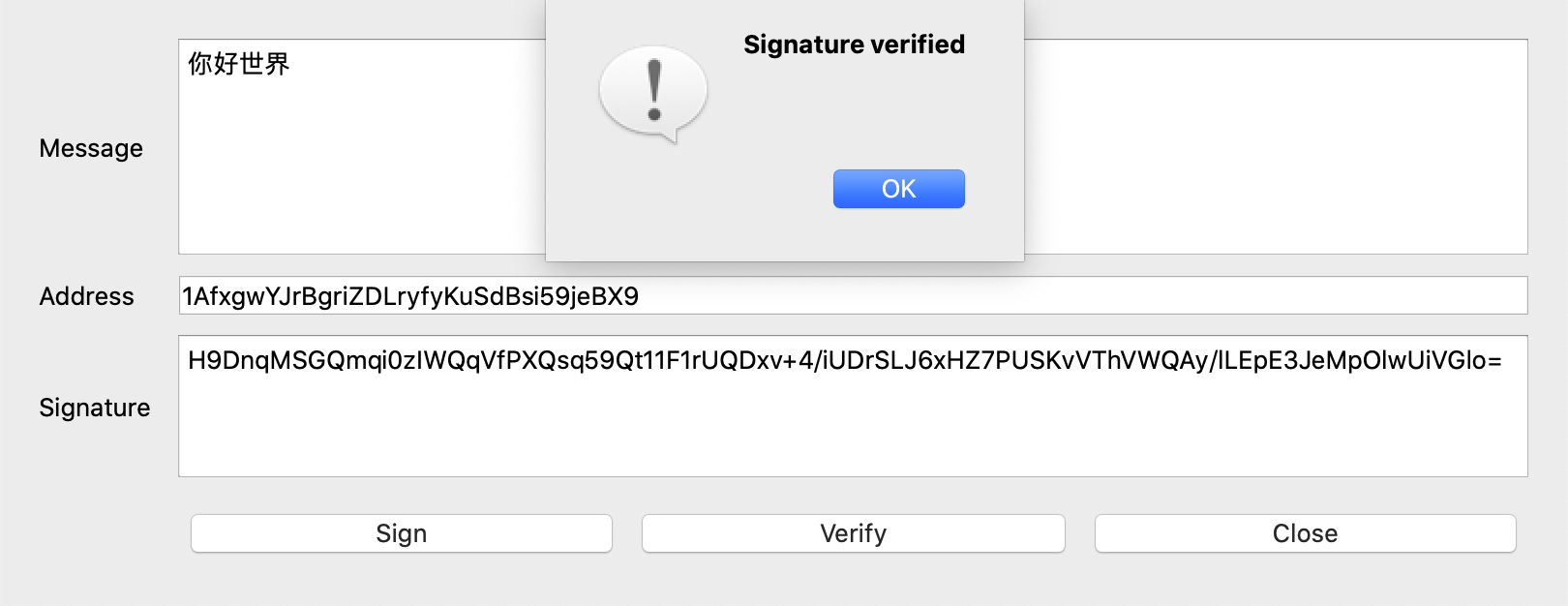
验签通过即可证明，该地址对应的私钥确实在我手上。请注意，要签名的消息，可以是你我事先商议好的任何内容，这里使用“你好世界”只是演示。

本文将详述如何使用比特币私钥对任意消息签名。

发现“问题”

你注意到没有，文章开头的证明信息里只包含地址、消息和签名，而没有公钥。

但验签操作需要公钥。

能从地址反推吗？不能。地址是公钥哈希的可逆编码，从公钥哈希无法反推公钥，因为哈希是单向运算。所以无法从地址计算公钥。

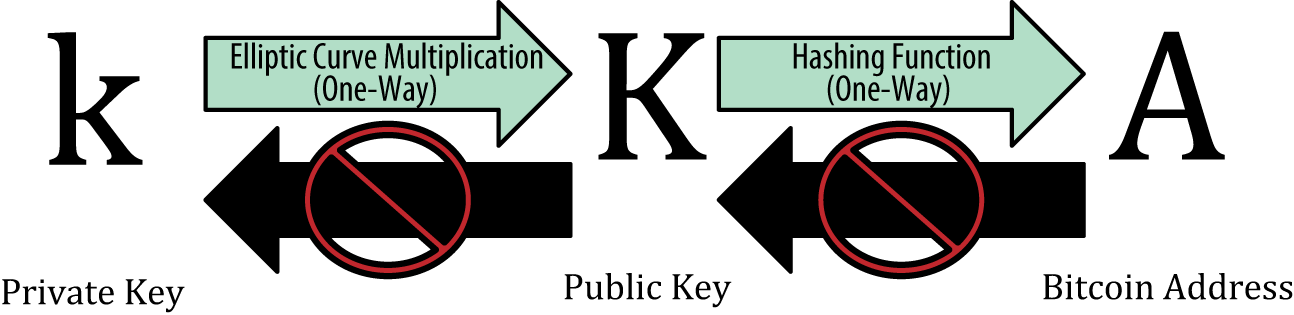
那么问题来了，没有公钥如何验签？只有一种可能，从 ECDSA 签名可以恢复公钥。

再说 ECDSA 签名

在介绍 ECDSA 时我们强调，签名过程中使用的临时私钥 $k$，保证其绝对私密且生成时足够随机非常重要。

签名和消息是公开的，即已知 $(r, s)$ 和 $e$，如果还知道 $k$，就可以算出私钥。

$$
a = r^{-1}(sk - e) \bmod{n}
$$

进一步的，如果知道的是 $K$，则可以算出公钥。

$$
A = aG = r^{-1}(sk - e) \cdot G = r^{-1}(s \cdot kG - eG) = r^{-1}(sK - eG)
$$

所以从签名恢复公钥的关键，是确定点 $K$ 的坐标 $(x_K, y_K)$。

注意到，对 Secp256k1 的参数 $n$ 和 $p$，有 $n < p$，而 $r = x_K \bmod{n}$。

所以从 $r$ 求 $x_K$，结果不一定唯一。当 $r + n < p$ 时，$x_K = r$ 和 $x_K = r + n$ 都是解。

另外，知道了 $x_K$ 也不能唯一确定 $y_K$。椭圆曲线是上下对称的，若点 $(x, y)$ 在曲线上，则点 $(x, -y \bmod{p})$ 也在曲线上。之前的文章在介绍比特币公钥时提到过，对 Secp256k1，至少要知道点的 X 坐标和 Y 坐标的奇偶，才能唯一确定该点。

让我们总结一下。如果想通过 ECDSA 签名 $(r, s)$ 和消息 $e$ 恢复公钥，还需要知道两个额外的信息：

  • $x_K$ 与 $n$ 的大小关系。若 $x_K < n$ 则 $x_K = r$，反之 $x_K = r + n$
  • $y_K$ 的奇偶性

Recoverable ECDSA 签名

这个“额外信息”只有四种状态，用 2 个二进制位即可表示。高位是 0 标记 $x_K < n$，低位是 0 标记 $y_K$ 的偶数。

二进制位 内容 十进制值
00 $x_K < n$，$y_K$ 是偶数 0
01 $x_K < n$，$y_K$ 是奇数 1
10 $x_K > n$，$y_K$ 是偶数 2
11 $x_K > n$，$y_K$ 是奇数 3

我们把这个标记，称为recovery_id或recid，把包含了此标记的 ECDSA 签名 $(recid, r, s)$，称为“可恢复”签名（recoverable ECDSA signature）或致密签名（compact signature）。

对应代码不难实现，只需在计算 $(r, s)$ 时同时计算recid即可。

def sign_recoverable(private_key: int, message: bytes) -> tuple:
    """Create recoverable ECDSA signature, aka compact signature, (recovery_id, r, s)"""
    e = hash_to_int(message)
    recovery_id, r, s = 0, 0, 0
    while not r or not s:
        k = random.randrange(1, curve.n)
        k_x, k_y = scalar_multiply(k, curve.g)
        # r
        r = k_x % curve.n
        recovery_id = 0 | 2 if k_x > curve.n else 0 | k_y % 2
        # s
        s = ((e + r * private_key) * modular_multiplicative_inverse(k, curve.n)) % curve.n
    return recovery_id, r, s

计算消息摘要

用私钥对交易签名，实际上是用私钥对交易摘要签名。类似的，对消息签名时，需要先计算消息的摘要，然后对消息摘要签名。

消息摘要有特定的格式。

项 内容
len(H) H 的字节长度，VarInt 类型表示，定值 0x18
H 字符串 Bitcoin Signed Message:\n 的 UTF-8 编码
len(M) M 的字节长度，VarInt 类型表示
M 消息 $m$ 的 UTF-8 编码 
def message_bytes(message: str) -> bytes:
    """Serialize plain text message to format (LEN || message.utf-8)"""
    msg_bytes = message.encode('utf-8')
    return int_to_varint(len(msg_bytes)) + msg_bytes


def message_digest(message: str) -> bytes:
    """Returns the digest of plain text message"""
    return message_bytes('Bitcoin Signed Message:\n') + message_bytes(message)

调用message_digest方法，就可以得到原始消息的消息摘要。

请注意，我们在计算“消息摘要”时并没有使用哈希方法，所以严格来说这个计算的结果不能叫消息的“摘要”，对整个转换过程更准确的描述应该是“消息的格式化”或“消息的序列化”。之所以也使用“摘要”这个词，是为了将它跟之前在介绍对交易签名时提到的“交易摘要”对应起来，方便你整体理解。

序列化签名结果

至此，所有的准备工作均已就绪，在展示最终结果前，还需要序列化。

签名 $(recid, r, s)$ 总会被序列化成 65 字节。

字节长度 内容
1 前缀信息
32 整数 r 按大端模式序列化后的字节流
32 整数 s 按大端模式序列化后的字节流

别忘了，比特币公钥有两种表示法，一种以 0x04 开头有 65 字节，另一种以 0x02 或 0x03 开头有 33 字节，即同一个公钥会对应两个 P2PKH 地址。为了能在验签时同时校验恢复出的公钥的哈希，是否与输入的地址相匹配，还需要在前缀信息里标记公钥的表示方式。

前缀的值 内容
27 + recid + 4 公钥用 33 字节表示
27 + recid + 0 公钥用 65 字节表示

最后，用 Base64 编码处理序列化后的签名数据，以方便人们复制和转录。

from base64 import b64encode


def sign_message(private_key: int, plain_text: str) -> tuple:
    """Sign arbitrary message with bitcoin private key, returns (p2pkh_address, serialized_compact_signature)"""
    d = message_digest(plain_text)
    # recovery signature
    recovery_id, r, s = sign_recoverable(private_key, d)
    # p2pkh address
    public_key = scalar_multiply(private_key, curve.g)
    p2pkh_address = public_key_to_address(public_key, compressed=True)
    # prefix = 27 + recovery_id + (4 if using compressed public key else 0)
    prefix = 27 + recovery_id + 4
    serialized_sig = prefix.to_bytes(1, byteorder='big') + r.to_bytes(32, byteorder='big') + s.to_bytes(32, byteorder='big')
    return p2pkh_address, b64encode(serialized_sig).decode('ascii')

我们写一个简单的例子来测试。

if __name__ == '__main__':
    # 私钥
    priv_key = 0xf97c89aaacf0cd2e47ddbacc97dae1f88bec49106ac37716c451dcdd008a4b62
    # 公钥
    pub_key = scalar_multiply(priv_key, curve.g)
    # 消息
    plain = '使用比特币私钥对任意消息签名 aaron67'
    print(plain)
    # 签名
    print(sign_message(priv_key, plain))

输出为

使用比特币私钥对任意消息签名 aaron67
('1AfxgwYJrBgriZDLryfyKuSdBsi59jeBX9', 'H87QAsj1vFPZBNBCyfJtOK2HW9IpM5Bio5zoeRoMr7Yb4Qr4//4X/C/Ah5d64Lq4P/5EKImfnAIW8x0zx74HQSs=')

使用钱包工具或第三方服务验证这个输出，可以验签成功。

验签

在验证对消息的签名时，输入变成了比特币地址、原始消息和序列化后的致密签名，所以对应的验签过程也要微调。

  1. 从序列化后的签名中，解析出recid和 $(r, s)$，同时明确公钥的表示方式
  2. 恢复公钥
  3. 用公钥和消息验证签名 $(r, s)$
  4. 验证恢复出的公钥的哈希，是否与输入的比特币地址相匹配

利用recid恢复公钥时，需要从点的 X 坐标求对应的 Y 坐标。对 Secp256k1 的曲线方程

$$
y^2 \equiv x^3 + 7 \pmod{p}
$$

知道了 $x$ 就等于知道了 $y^2 \bmod{p}$，为了求 $y$，需要“开方”，这很麻烦，因为有模运算。我们可以用费马小定理来改进。

对整数 $a$ 和质数 $p$，有

$$
a^p \equiv a \pmod{p}
$$

曲线 Secp256k1 的 $p$ 是一个质数，所以有

$$
y^{p} \equiv y \pmod{p}
$$

利用同余关系的性质，将上式两边同时放大 $y$ 倍，有

$$
y^{p+1} \equiv y^2 \pmod{p}
$$

即

$$
(y^2)^{\frac{p+1}{2}} \equiv y^2 \pmod{p}
$$

则

$$
y = (y^2)^{\frac{p+1}{4}} \bmod{p}\ \ \ \ 或\ \ \ \ -(y^2)^{\frac{p+1}{4}} \bmod{p}
$$

注意到，$\frac{p+1}{4}$ 是一个整数。也就是说，通过计算 $y^2$ 的整数次幂，就可以求解 $y$。

有了这些知识，不难写出对应的验签代码，请注意求解point_k时对费马小定理的应用。

def verify_message(p2pkh_address: str, plain_text: str, signature: str) -> bool:
    """Verify serialized compact signature with p2pkh address and plain text"""
    sig_bytes = b64decode(signature)
    if len(sig_bytes) != 65:
        return False
    prefix, r, s = sig_bytes[0], int.from_bytes(sig_bytes[1:33], byteorder='big'), int.from_bytes(sig_bytes[33:], byteorder='big')
    # Calculate recovery_id
    compressed = False
    if prefix < 27 or prefix >= 35:
        return False
    if prefix >= 31:
        compressed = True
        prefix -= 4
    recovery_id = prefix - 27
    # Recover point kG, k is the ephemeral private key
    x = r + (curve.n if recovery_id >= 2 else 0)
    y_squared = (x * x * x + curve.a * x + curve.b) % curve.p
    y = pow(y_squared, (curve.p + 1) // 4, curve.p)
    if (y + recovery_id) % 2 != 0:
        y = -y % curve.p
    point_k = (x, y)
    # Calculate point aG, a is the private key
    d = message_digest(plain_text)
    e = hash_to_int(d)
    mod_inv_r = modular_multiplicative_inverse(r, curve.n)
    public_key = add(scalar_multiply(mod_inv_r * s, point_k), scalar_multiply(mod_inv_r * (-e % curve.n), curve.g))
    # Verify signature
    if not verify_signature(public_key, d, (r, s)):
        return False
    # Check public key hash
    if public_key_hash(public_key, compressed) != address_to_public_key_hash(p2pkh_address):
        return False
    # OK
    return True

我们用其他工具生成的签名作为输入，来检验验签代码的正确性。将私钥导入 ElectrumSV 钱包对消息签名，可以得到结果

IGdzMq98lowek10e3JFXWj909xp0oLRj71aF7jpWRxaabwH+fBia/K2JpoGQlFFbAl/Q5jo2DYSzQw6pZWhmRtk=

调用验签方法测试。

if __name__ == '__main__':
    # 私钥
    priv_key = 0xf97c89aaacf0cd2e47ddbacc97dae1f88bec49106ac37716c451dcdd008a4b62
    # 公钥
    pub_key = scalar_multiply(priv_key, curve.g)
    # 地址
    address = public_key_to_address(pub_key, compressed=True)
    # 消息
    plain = '使用比特币私钥对任意消息签名 aaron67'
    # 验证签名
    sig_electrum = 'IGdzMq98lowek10e3JFXWj909xp0oLRj71aF7jpWRxaabwH+fBia/K2JpoGQlFFbAl/Q5jo2DYSzQw6pZWhmRtk='
    print(verify_message(address, plain, sig_electrum))

运行结果为

True

输出符合预期。

完整代码

sign_message.py

参考